급질문 입니다..산수 문제
2010.11.12 10:36
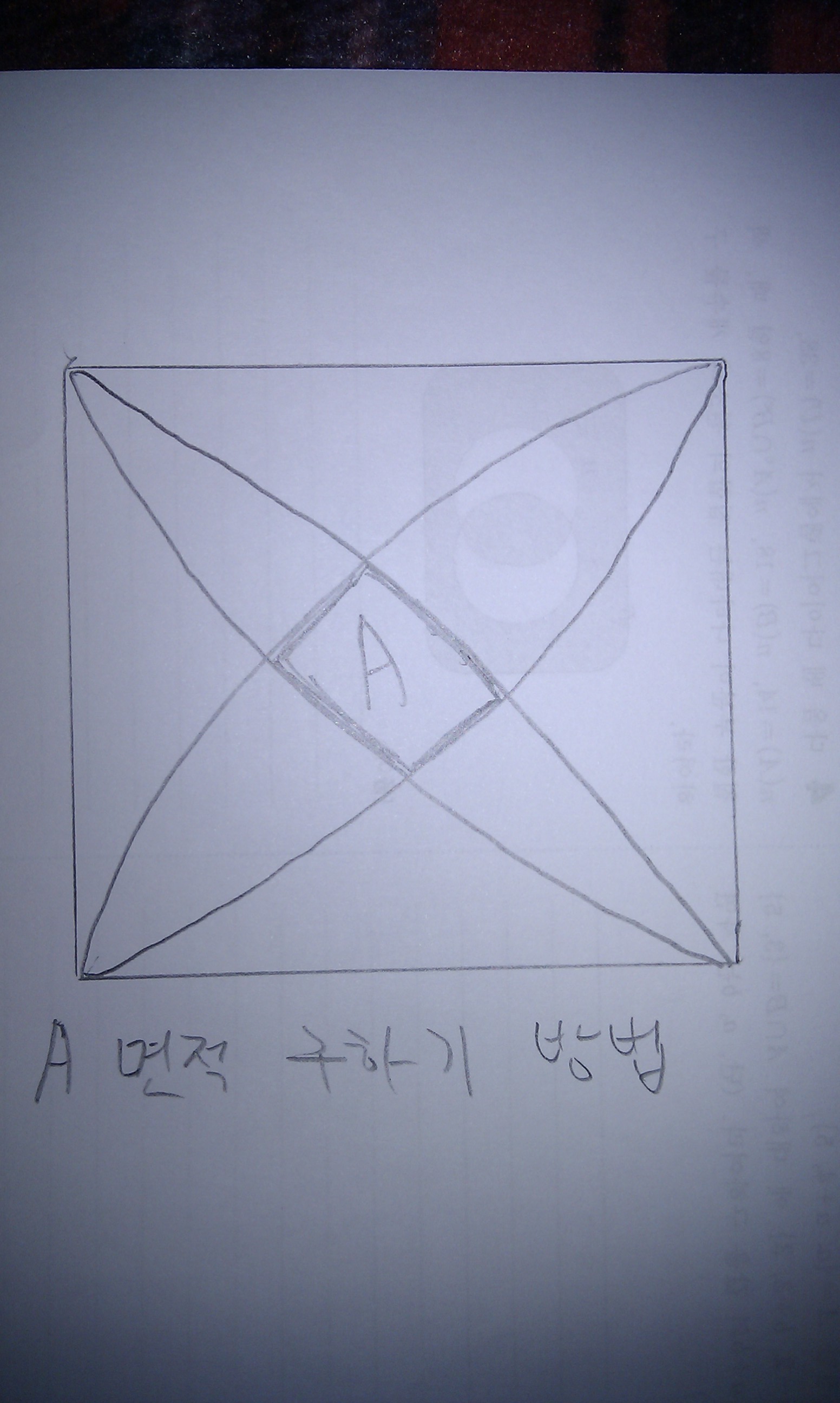
면적구하는 방법 좀 알려 주세요~
감사합니다.
댓글 [12]
-
OLokLiR 2010.11.12 10:53
-
우금티 2010.11.12 10:54 원의 반경에 대한 정보가 없어서 구할 수 없습니다...
그림으로 보면 원의 반경이 정사각형의 한 변과 같지 않을 듯해서 말이죠...반경=한변 이라면..
사각형으로부터 빼 나가는 방법으로는 구할 수 없을 듯합니다..
오히려 중복을 허용해서 더해가면서 최종적으로 사각형보다 훨씬 큰 값으로 계산을 마치면,
사각형 면적을 초과한 값은 구하고자 하는 면적이 3번 중첩되고.. B면적과 C면적이 각각 두번 중첩되고..
이런식으로 계산을 풀면... 원하는 값을 얻으리라 보여집니다. -
펔탄 2010.11.12 11:02
제가 젬뱅이라 알아듣지도 못하고 보여주기만 하네요... 근데 모르겠데요~... 설명서를 봐야하나 아님 정석을 보여줘야하나..
답답하네요~ 직사각형이라고 햇다는데..중1 문제가 일케 나와요.? 선생을 잡아 팰까..
-
jsy090 2010.11.12 11:56 A를 교점 4개를 이은 사각형 과 나머지 활꼴4개 넓이의 합으로 구할수 있을거같습니다.
-
쿨에딧 2010.11.12 13:29
수학은 대입이후 손을 놨지만 저건 구체적인 면적을 구할 수 있는 값(이라해야되나?)이 없이 그냥 구할수 있는것인지?
-
꿈의 별 2010.11.12 16:23
'7나'에서 나오는 문제로군요 (중학교 1학년 2학기에서 4점짜리 문제로 자주 출제됩니다..ㄷㄷ)
-
펔탄 2010.11.12 22:09
출제가 되긴 하는가보네요~ 혼자 선생욕만 열라 햇거든요,,
국민학교서 얼마나 잘배우길래 이런문제가 나오냐고 마눌한티 따졋거든요,,
-
맨맨 2010.11.12 21:12
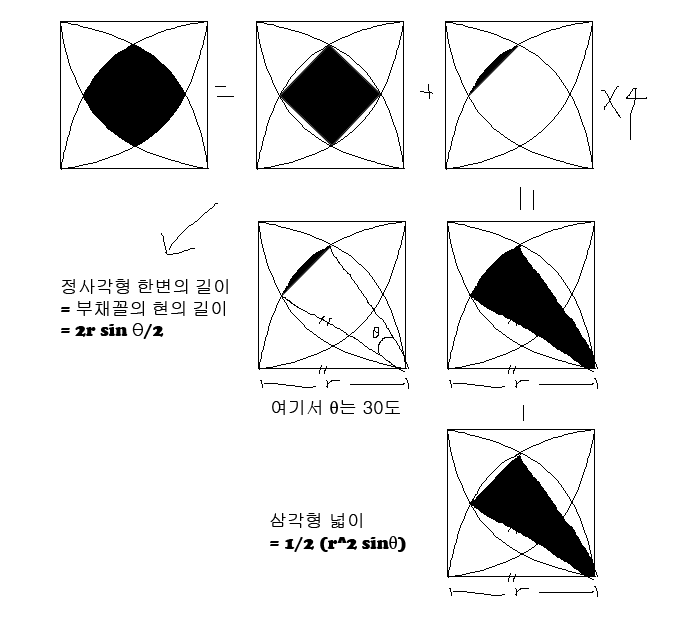
대략 개념은 이렇게 될것 같은데 배운지 오래되어서 결과 계산이 잘 안되는군요.^^;
-
펔탄 2010.11.12 22:07
감사합니다..역시 실력자 분들이 많으시네요~전 배운건지도 생각이 않납니다..
ㅠㅠ
-
개나리 2010.11.13 12:06 어이구 뭔소리들 하시는지 하나도 모르겠당. ㅆ.ㅆ;
-
구경중 2010.11.15 09:19 이런 문제는 과감히 틀렸...;;;
-
Egofinder 2010.11.15 09:58
정사각형의 한변의 길이가 왜 부채꼴의 현의 길이와 같죠?? 어렵네요.
저는 적분으로 구했는데.(일반 X,Y 좌표계입니다. r은 사각형 한변의 길이입니다.
1. (X-r)^2 + Y^2 = r^2
2. Y = 1/2*r
방정식 풀어서 X 값을 구합니다.(a라고 하면)
그럼 적분구간이 (a, 1/2*r) 로 정해집니다.1. 방정식을 Y에 관하여 풀고 적분으로 정리해줍니다.
(a,1/2*r)의 적분구간에서 y축의 상수함수 1/2*r 를 빼주면. 1/4의 면적이 나옵니다.
4배합니다.
4개의 교점이 사각형을 정확이 이등분하는 지점에서 만나는지 증명해야 하는데 그건 잘 모르겠네요.
| 번호 | 제목 | 글쓴이 | 조회 | 등록일 |
|---|---|---|---|---|
| [공지] | 자유 게시판 이용간 유의사항 (정치, 종교, 시사 게시물 자제) [1] | gooddew | - | - |
| 7249 | 케이스를 구매할려고하는데요..뭐가좋을가요 [3] |
|
2196 | 11-19 |
| 7248 | 아...감기들엇나봐요..ㅜㅜ [4] |
|
2179 | 11-18 |
| 7247 | 2011 년도 수능 c언어 영역 ~~~ [11] |
|
3203 | 11-18 |
| 7246 | 회원 여러분~ 좀 도와주십시요. [2] |
|
2607 | 11-18 |
| 7245 | 어떤 게시판에 모태솔로란 말이 있길래.. [4] |
|
2784 | 11-17 |
| 7244 | 구인-사이트 개발자 및 관리자(웹 프로그래머) | 헤헤헤 | 2426 | 11-17 |
| 7243 | 아이패드 사전가입 했습니다. [7] |
|
2232 | 11-17 |
| 7242 | 참좋은여행 에서 중국여행을 다녀왔습니다..ㅠㅠ [7] |
|
2461 | 11-17 |
| 7241 | 반성도 되고 가슴에 와닿는 글이라 한번 올려봅니다. [4] |
|
2419 | 11-16 |
| 7240 | 콜오브듀티 블랙옵스 하시나여?? [2] |
|
2658 | 11-16 |
| 7239 | 스마트폰 활성화된 사이트 추천좀 해주세요. [2] |
|
2450 | 11-16 |
| 7238 | 하드검사결과 괜찮은건가요?? [5] | 난방 보일 | 2658 | 11-16 |
| 7237 | 음악재생기 추천 부탁드립니다 [11] | 도라란 | 3085 | 11-16 |
| 7236 | 갤럭시폰 프로요 업데이트 되시나요? [8] |
|
3119 | 11-15 |
| 7235 | 아따...디비디 왤캐 삑이 잘나나요... [7] |
|
2346 | 11-15 |
| 7234 | 카스퍼스키 방화벽.. 어렵네요.. [6] |
|
3651 | 11-15 |
| 7233 | win 7 HPQY A 10 구합니다 | 훈장 | 2457 | 11-15 |
| 7232 | 왜 개인의 생각에 "객관성"이 있어야 하죠? [25] |
|
10003 | 11-14 |
| 7231 | 블루레이 쓰기후 레코딩 실패가 항상 나네요. [3] |
|
3001 | 11-14 |
| 7230 | 지갑 추천해주세요 ㅎㅎ [7] |
|
2727 | 11-14 |

...; 순간 여기 지식인인줄;;;
r을 정사각형의 한변의 길이이자 원의 반지름이라 하고...
x^2+y^2=r^2를 y에 대해 정리한 다음
[적분시작] = 0.5r 이라하고,
[적분끝]을 구해야하는데, 처음 방정식에 y=0.5r 집어넣고 x에 대한 방정식을 만들어서 x값을 구해 나온 양의 x값을 [적분끝]으로 함
그럼 y로 정리한 원의 방정식을 [적분시작]부터 [적분끝]까지 x에 대해 적분한 뒤
직사각형 넓이 ([적분끝]-[적분시작])*0.5r을 계산한 적분값에서 빼면 저 영역의 1/4영역의 넓이가 나오지 싶습니다.