급질문 입니다..산수 문제
2010.11.12 10:36
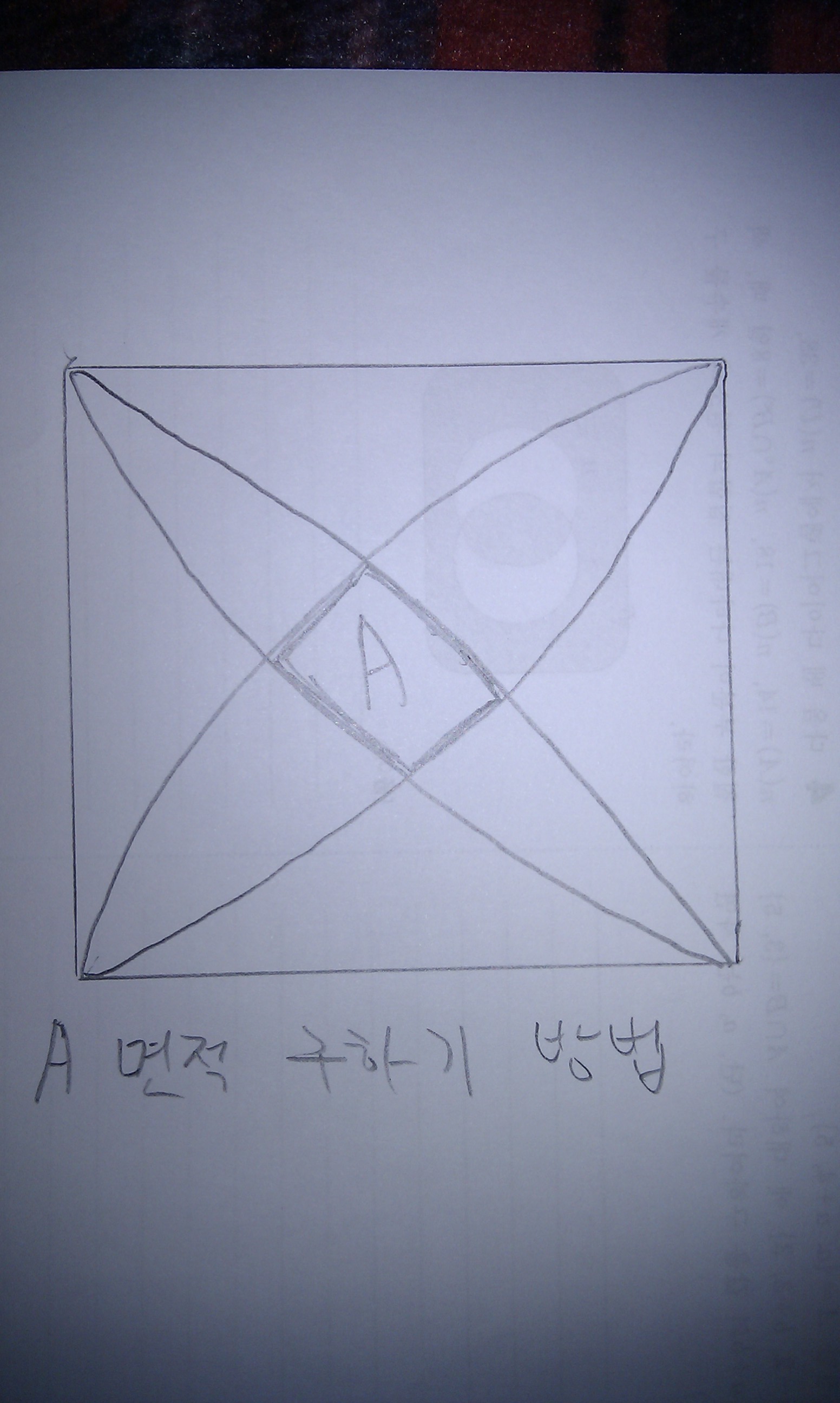
면적구하는 방법 좀 알려 주세요~
감사합니다.
댓글 [12]
-
OLokLiR 2010.11.12 10:53
-
우금티 2010.11.12 10:54 원의 반경에 대한 정보가 없어서 구할 수 없습니다...
그림으로 보면 원의 반경이 정사각형의 한 변과 같지 않을 듯해서 말이죠...반경=한변 이라면..
사각형으로부터 빼 나가는 방법으로는 구할 수 없을 듯합니다..
오히려 중복을 허용해서 더해가면서 최종적으로 사각형보다 훨씬 큰 값으로 계산을 마치면,
사각형 면적을 초과한 값은 구하고자 하는 면적이 3번 중첩되고.. B면적과 C면적이 각각 두번 중첩되고..
이런식으로 계산을 풀면... 원하는 값을 얻으리라 보여집니다. -
펔탄 2010.11.12 11:02
제가 젬뱅이라 알아듣지도 못하고 보여주기만 하네요... 근데 모르겠데요~... 설명서를 봐야하나 아님 정석을 보여줘야하나..
답답하네요~ 직사각형이라고 햇다는데..중1 문제가 일케 나와요.? 선생을 잡아 팰까..
-
jsy090 2010.11.12 11:56 A를 교점 4개를 이은 사각형 과 나머지 활꼴4개 넓이의 합으로 구할수 있을거같습니다.
-
쿨에딧 2010.11.12 13:29
수학은 대입이후 손을 놨지만 저건 구체적인 면적을 구할 수 있는 값(이라해야되나?)이 없이 그냥 구할수 있는것인지?
-
꿈의 별 2010.11.12 16:23
'7나'에서 나오는 문제로군요 (중학교 1학년 2학기에서 4점짜리 문제로 자주 출제됩니다..ㄷㄷ)
-
펔탄 2010.11.12 22:09
출제가 되긴 하는가보네요~ 혼자 선생욕만 열라 햇거든요,,
국민학교서 얼마나 잘배우길래 이런문제가 나오냐고 마눌한티 따졋거든요,,
-
맨맨 2010.11.12 21:12
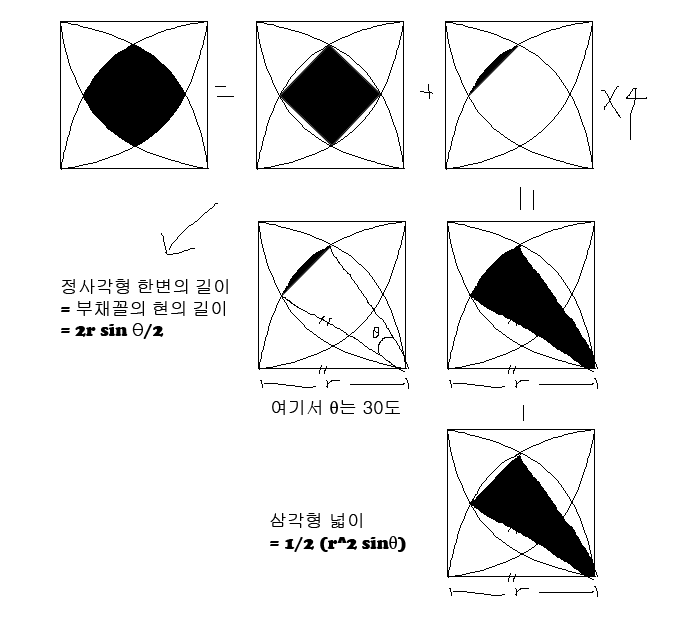
대략 개념은 이렇게 될것 같은데 배운지 오래되어서 결과 계산이 잘 안되는군요.^^;
-
펔탄 2010.11.12 22:07
감사합니다..역시 실력자 분들이 많으시네요~전 배운건지도 생각이 않납니다..
ㅠㅠ
-
개나리 2010.11.13 12:06 어이구 뭔소리들 하시는지 하나도 모르겠당. ㅆ.ㅆ;
-
구경중 2010.11.15 09:19 이런 문제는 과감히 틀렸...;;;
-
Egofinder 2010.11.15 09:58
정사각형의 한변의 길이가 왜 부채꼴의 현의 길이와 같죠?? 어렵네요.
저는 적분으로 구했는데.(일반 X,Y 좌표계입니다. r은 사각형 한변의 길이입니다.
1. (X-r)^2 + Y^2 = r^2
2. Y = 1/2*r
방정식 풀어서 X 값을 구합니다.(a라고 하면)
그럼 적분구간이 (a, 1/2*r) 로 정해집니다.1. 방정식을 Y에 관하여 풀고 적분으로 정리해줍니다.
(a,1/2*r)의 적분구간에서 y축의 상수함수 1/2*r 를 빼주면. 1/4의 면적이 나옵니다.
4배합니다.
4개의 교점이 사각형을 정확이 이등분하는 지점에서 만나는지 증명해야 하는데 그건 잘 모르겠네요.
| 번호 | 제목 | 글쓴이 | 조회 | 등록일 |
|---|---|---|---|---|
| [공지] | 자유 게시판 이용간 유의사항 (정치, 종교, 시사 게시물 자제) [1] | gooddew | - | - |
| 7664 | SP1 설치했습니다. [10] | ryder | 2756 | 01-15 |
| 7663 | 수영장 미끄럼타다가 다보여주네.. [1] |
|
2313 | 01-15 |
| 7662 | 무선랜 공짜로사용하시는분 중 [6] |
|
2469 | 01-14 |
| 7661 | SSD라... [6] | 스퀴니 | 1668 | 01-14 |
| 7660 | [회원탐구] 만사형통 4 [14] |
|
1716 | 01-14 |
| 7659 | 제 노트북사양이... [5] | 스퀴니 | 1295 | 01-14 |
| 7658 | 애플에서 오늘만 할인행사하네요.. [2] |
|
1356 | 01-14 |
| 7657 | 아프리카 tv 포터블 만들어 봤는대 대는지.. [1] | Ohys | 3779 | 01-14 |
| 7656 | File Renamer Turbo 한글화가 안되요. ㅠㅠ; [2] |
|
1286 | 01-14 |
| 7655 | sk 브로드벤드쓰시는 분들...... [15] | 딸기 | 3709 | 01-14 |
| 7654 | 아무리 생각해봐도... [5] |
|
1698 | 01-13 |
| 7653 | 닉네임 고달픈명탐정님께 [2] | 갈밭 | 1877 | 01-13 |
| 7652 | MS 인증 메뉴얼 검수 및 보완 좀 부탁드립니다. [15] | 공피 | 10396 | 01-13 |
| 7651 | 돈 흐름에 문제가 있군요 [5] | 짜장면 | 2243 | 01-13 |
| 7650 | 곰녹음기 | 엘에이맨 | 1420 | 01-13 |
| 7649 | 크래들 타입 외장하드 사실 계획 있으신분들 참조하세요~ [5] | 도라란 | 1917 | 01-13 |
| 7648 | 뭐 딴 얘기지만 mac버전은 오피스2011이 나왔군요.. [6] |
|
2070 | 01-12 |
| 7647 | '로봇 영재' 죽음으로 내몬 사회 [4] |
|
1686 | 01-12 |
| 7646 | 자료 좀 찾아주세요... [6] |
|
1495 | 01-12 |
| 7645 | 이야기 와전 [7] |
|
1313 | 01-12 |

...; 순간 여기 지식인인줄;;;
r을 정사각형의 한변의 길이이자 원의 반지름이라 하고...
x^2+y^2=r^2를 y에 대해 정리한 다음
[적분시작] = 0.5r 이라하고,
[적분끝]을 구해야하는데, 처음 방정식에 y=0.5r 집어넣고 x에 대한 방정식을 만들어서 x값을 구해 나온 양의 x값을 [적분끝]으로 함
그럼 y로 정리한 원의 방정식을 [적분시작]부터 [적분끝]까지 x에 대해 적분한 뒤
직사각형 넓이 ([적분끝]-[적분시작])*0.5r을 계산한 적분값에서 빼면 저 영역의 1/4영역의 넓이가 나오지 싶습니다.